brain of mat kelcey...

the jaccard coefficient is one of the fundamental measures for doing set similarity.

( recall jaccard(set1, set2) = |intersection| / |union|. when set1 == set2 this evaluates to 1.0 and when set1 and set2 have no intersection it evaluates to 0.0 )

one thing that's always annoyed me about it though is that is loses any sense of partial similarity. as a set based measure it's all or nothing.

so consider the sets set1 = {i1, i2, i3} and set2 = {i1, i2, i4}

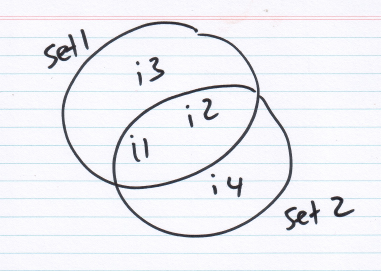
jaccard(set1, set2) = 2/4 = 0.5 which is fine given you have no prior info about the relationship between i3 and i4.

but what if you have a similarity function, s, and s(i3, i4) ~= 1.0? in this case you don't want a jaccard of 0.5, you want something closer to 1.0. by saying i3 ~= i4 you're saying the sets are almost the same.

after lots of googling i couldn't find a jaccard variant that supports this idea so i rolled my own. the idea is that we want to count the values in the complement of the intersection not as 0.0 on the jaccard numerator but as some value ranging between 0.0 and 1.0 based on the similarity of the elements. after some experiments i found that just counting each as the root mean sqr value of the pairwise sims of them all works pretty well. i'd love to know the name of this technique (or any similar better one) so i can read some more about it.

def fuzzy_jaccard(s1, s2, sim):
    union = s1.union(s2)
    intersection = s1.intersection(s2)

    # calculate root mean square sims between elements in just s1 and just s2
    just_s1 = s1 - intersection
    just_s2 = s2 - intersection
    sims = [sim(i1, i2) for i1 in just_s1 for i2 in just_s2]
    sqr_sims = [s * s for s in sims]
    root_mean_sqr_sim = sqrt(float(sum(sqr_sims)) / len(sqr_sims))

    # use this root_mean_sqr_sim to count these values in the complement as, in some way, being "partially" in the intersection
    return float(len(intersection) + (root_mean_sqr_sim * intersection_complement_size)) / len(union)

looking at our example of {i1, i2, i3} vs {i1, i2, i4}...

when s(i3, i4) = 0.0 it degenerates to normal jaccard and scores 0.5

print fuzzy_jaccard(set([1,2,3]), set([1,2,4]), lambda i1, i2: 0.0)  # = 0.5 (2/4)  ie normal jaccard

when s(i3, i4) = 1.0 it treats the values as the same and scores 1.0

print fuzzy_jaccard(set([1,2,3]), set([1,2,4]), lambda i1, i2: 1.0)  # = 1.0 (4/4)  treating i3 == i4

when s(i3, i4) = 0.9 it scores inbetween with 0.8

print fuzzy_jaccard(set([1,2,3]), set([1,2,4]), lambda i1, i2: 0.8)  # = 0.9 (3.6/4)

this is great for me because now given an appropriate similiarity function i'm able to get a lot more discrimination between sets.