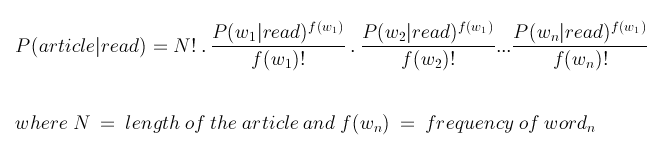
multi nominal bayes is a variation of naive bayes that considers not the frequency of articles of a class but the frequencies of the words in a class
let's revisit our test data from the last experiment, with some slight variatons
| text | feed | should read it? |
| linux on the linux | the register | yes (rule 1) |
| cat on ferrari | autoblog | no |
| on the hollywood | perezhilton | no |
| on lamborghini on cat | autoblog | yes (rule 2) |
| hollywood cat | perezhilton | no |
| the lamborghini | perezhilton | yes (rule 2) |
| cat on linux cat | the register | yes (rule 1) |
considering just a few words this breaks down to
| word | totaloccurences | number in should read | number inshould ignore |
| on | 6 | 4 | 2 |
| linux | 3 | 3 | 0 |
| the | 3 | 2 | 1 |
| hollywood | 2 | 0 | 2 |
| 9 | 5 |
from this table we have some various word / class related probabilities including... P('on' | read) = 4/9 = 44% P('linux' | ignore) = 0/5 = 0%
we can use a multinomial distribution to determine the probability for a given test article
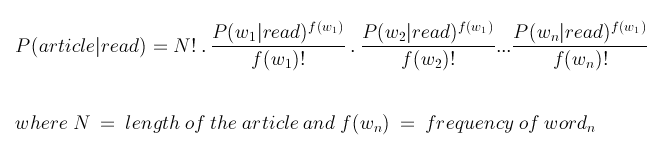
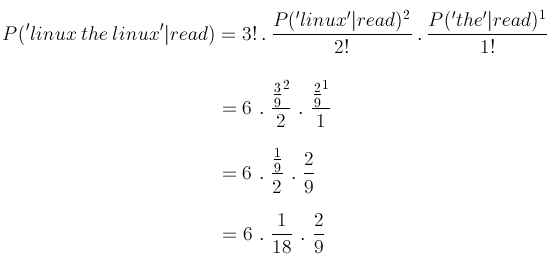which is 7.5%
and for the same article, 'linux the linux', we have probabiltiy of should ignore being
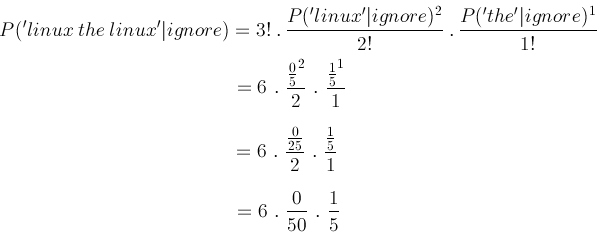which is strictly 0% but using a laplace estimator (as seen in last experiment) we have
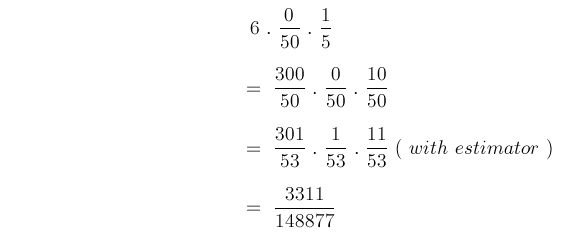which is 2.2%, less than the should read probability, so the classifier would recommend we read this article
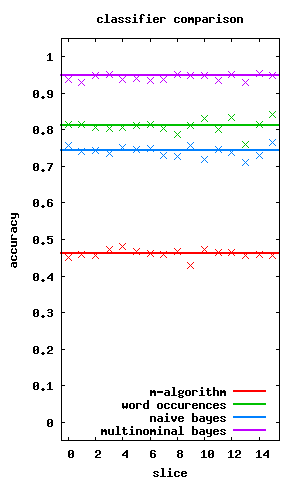
so how does this algorithm run against the 13,500 articles we have for theregister, perezhilton and autoblog then? whereas naive bayes did worse than the simple word occurences, the multinomial bayes kicks ass!
the graph to the left shows the accuracy of the three classification algorithms we discussed so far (thick lines denote the median performance of the algorithm over a number of runs crosses denote a cross validation run)
well i've had enough of bayes, lets try a classifier based on markov chains!
view the code at github.com/matpalm/rss-feed-experiments