brain of mat kelcey...

( with a fun exploration of easy/hard positive/negative mining )

brutually short introduction to triplet loss

say we want to train a neural net whose output is an embedding of its input. how would we train it?

to train anything we need a loss function and usually that function describes exactly what we want the output to be in the form of explicit labels. but for embeddings things are a little different. we might not care exactly what embedding values we get, we only care about how they are related for different inputs.

one way of specifying this relationship for embeddings is with an idea called triplet loss.

let's consider three particular instances...

1. a random instance (we'll call this the anchor)
2. another instance that is somehow related to the anchor and, as such, we want close in the embedding space (we'll call this the positive)
3. a third instance that is somehow different to the anchor that we don't want close in the embedding space (we'll call this the negative)

triplet loss is a way of specifying that we don't care exactly where things get embedded, only that the anchor should be closer to the positive than to the negative.

we can express this idea of closer in a loss function in a simple clever way...

consider two distances; the distance from the anchor to the positive (dist_anchor_positive) and the distance from the anchor to the negative (dist_anchor_negative)

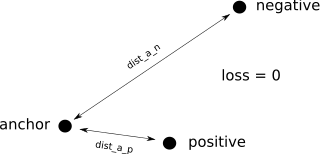
if dist_anchor_positive < dist_anchor_negative it means the positive is closer to the anchor than the negative. this is good, and what we want from our embedding so things shouldn't change; i.e. should be a loss of zero.

if dist_anchor_positive < dist_anchor_negative:
  loss = 0

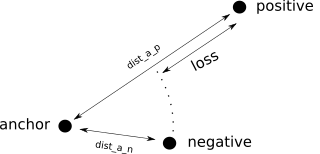
if dist_anchor_positive > dist_anchor_negative though it means the positive is further from the anchor than the negative. this is bad, we should adjust these embeddings. but how much loss should we attribute to this case? turns out we can literally just use the difference in these distances! i.e. a little bit of loss if the difference is low, but a larger loss otherwise.

if dist_anchor_positive > dist_anchor_negative:
  loss = dist_anchor_positive - dist_anchor_negative

good	bad

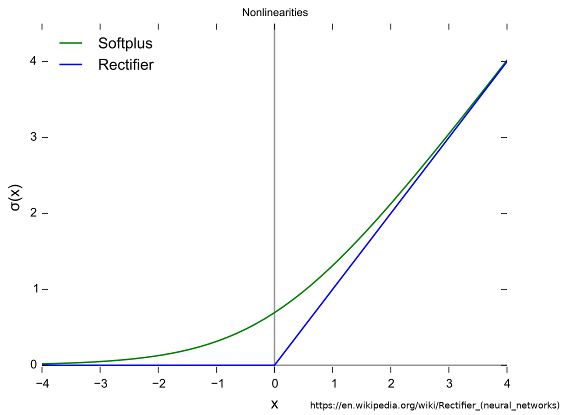
these two cases can be combined very elegantly using a max with 0.

loss = max(0, dist_anchor_positive - dist_anchor_negative)

this loss is (unsurprisingly) known as hinge loss and has a close relationship with relu & softplus

relu and softplus

a final point is that to encourage more seperation we might say that not only does the positive have to be closer, it has to be closer by some fixed amount. we call this a margin

grasping in pybullet

let's put triplet loss aside for a bit and consider robotic grasping. we might not be able to afford a physical robot but there's a lot we can play with in simulation.

with pybullet we can simulate a grasping setup easily! e.g. consider the following...

• a simple grasping environment of a table + a tray + an arm
• 15 procedurally generated objects dropped into the tray
• a sequence of random grasps

where a random grasp is ...

1. move gripper to random point above tray
2. move gripper down into tray
3. close gripper
4. move gripper up again (& fingers crossed we got something :)

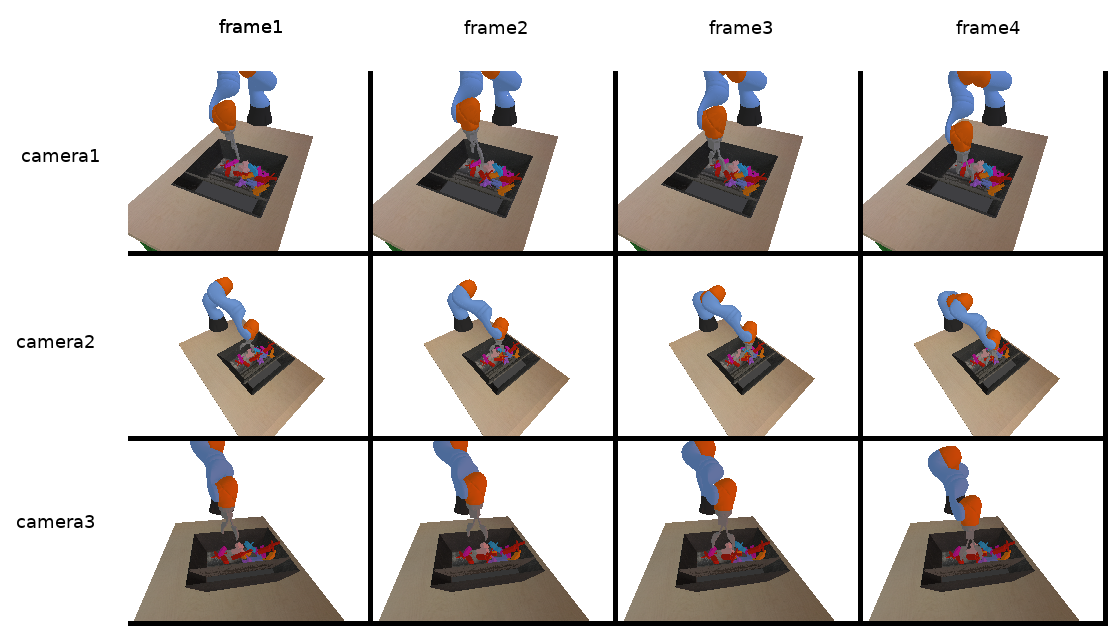
during this sequence we can capture the environment by rendering the view from 90 randomly placed cameras every 20 steps of the simulation and continue random grasping until we have 1000 images.

different camera views from some random grasping

time contrastive networks

given this grasping setup could we learn an embedding of camera images that represents something about the scene that is agnostic to the specific camera view?

we'd want this embedding to have a mapping that is the same when the scene is the same, regardless of the camera angle & have a mapping that is different when the scene is different, again regardless of the camera angle. if only we had a way of describing a loss function for these kinds of pairings!

wait. a.. minute... triplet loss!!!

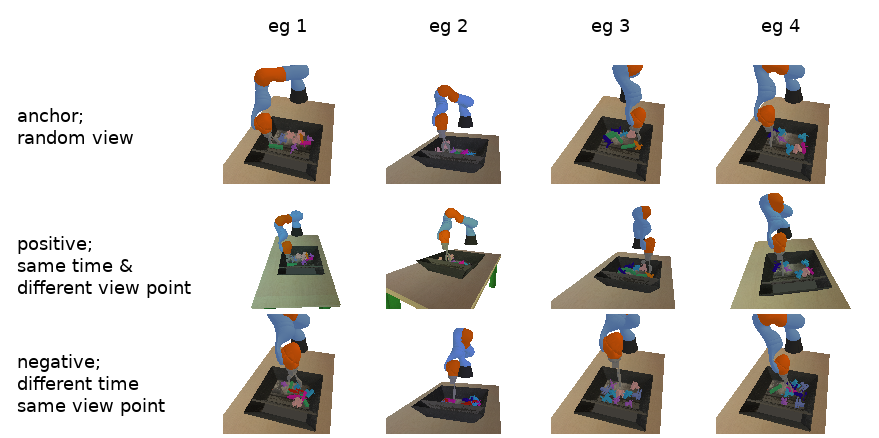
the idea of doing this was first introduced in the paper Time-Contrastive Networks: Self-Supervised Learning from Video by Pierre and co. and in this formulation...

• the anchor is a camera image from a random view point at a random time
• the positive is a camera image from a different view point but at the same time
• the negative is a camera image from the same view point but at a different time

an example batch of four triples is the following...

training

let's train a very simple small model for this experiment. ( the training data and loss function is more interesting than a huge model and for i saw marginal improvement in a bigger model anyway... )

______________________________________________________________________________________
Layer (type)                 Output Shape              Param #  Comment
======================================================================================
inputs (InputLayer)          (None, 180, 240, 3)       0
conv2d (Conv2D)              (None, 90, 120, 16)       1216    # 5x5 stride 2
conv2d_1 (Conv2D)            (None, 45, 60, 32)        4640    # 3x3 stride 2
conv2d_2 (Conv2D)            (None, 23, 30, 32)        9248    # 3x3 stride 2
conv2d_3 (Conv2D)            (None, 12, 15, 32)        9248    # 3x3 stride 2
flatten (Flatten)            (None, 5760)              0
dropout (Dropout)            (None, 5760)              0       # keep = 0.5
dense (Dense)                (None, 64)                368704
embedding (Dense)            (None, 128)               8320
normalise_layer (NormaliseLa (None, 128)               0       # tf.nn.l2_normalize
======================================================================================
Total params: 401,376
Trainable params: 401,376

for the loss function we do as described above... (note: a batch of B training instances is 3*B images; each instance is a triple of images)

embeddings = model.output                                            # (3B, E)
embeddings = tf.reshape(embeddings, (-1, 3, embedding_dim))          # (B, 3, E)
anchor_embeddings = embeddings[:, 0]                                 # (B, E)
positive_embeddings = embeddings[:, 1]                               # (B, E)
negative_embeddings = embeddings[:, 2]                               # (B, E)
dist_a_p = tf.norm(anchor_embeddings - positive_embeddings, axis=1)  # (B)
dist_a_n = tf.norm(anchor_embeddings - negative_embeddings, axis=1)  # (B)
constraint = dist_a_p - dist_a_n + margin                            # (B)
per_element_hinge_loss = tf.maximum(0.0, constraint)                 # (B)
return tf.reduce_mean(per_element_hinge_loss)                        # (1)

evaluation

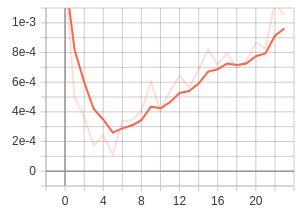
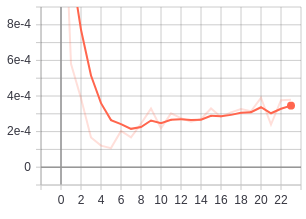
during training there are a number of interesting things to keep track of...

firstly the relationship between dist_a_p and dist_a_n. when things are going well we want the dist_a_n to be constantly outgrowing dist_a_p

distance anchor negative	distance anchor positive

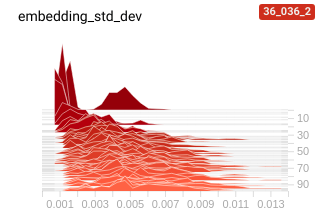
an interesting failure case, especially when the margin is too low, is that the model just learns to map everything to the same point ( i.e. dist_a_p - dist_a_n is minimised well when all the distances are zero :/)

this is very visible when we eyeball the distribution of embeddings for some held out data

good spread of embeddings	collapsed embeddings

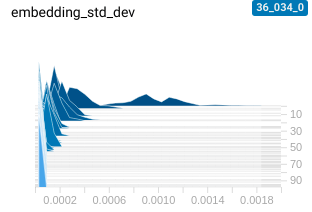
but apart from the distribution of embeddings, are there other ways to evaluate the embeddings?

one way is to compare the embeddings of a scene from some held out data. given we know the camera positions we can consider a reference grasp sequence of N frames and find the near neighbours, in the embedded space, from two other target_a and target_b camera views. we select near neighbours for target_a and target_b from different runs than the reference to ensure it's not just picking up exact matches.

embedding near neighbours on held out data

we can see visually that the pose of the arms generally match.

trouble is eyeballing things isn't really quantifiable; is there a number we can look at?

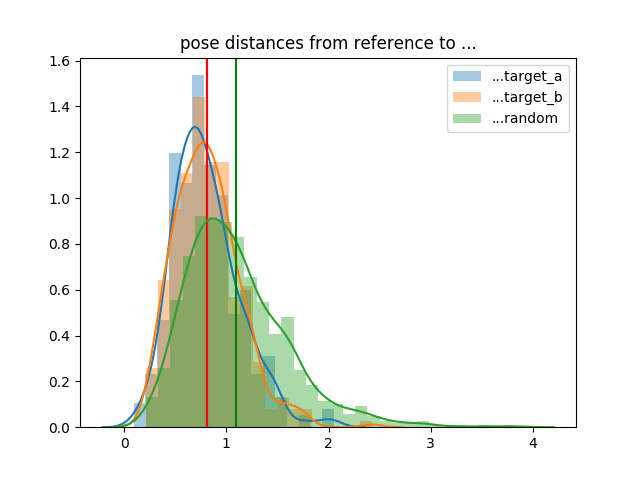
one numerical attribute we have of the scene is the position of the arm in joint space (i.e. the seven joint angles). what we can do is find the near neighbours in the embedding space based on the image but then compare based on the joint positions. one very simple (naive) comparison of the positions is their euclidean distance.

the following plot shows the distribution of joint distances between positions in the reference sequence and the near neighbour target_a and target_b frames. as a comparison point we also include the distribution of distances of random pairs (in green). vertical lines represent the mean values (note: the mean for target_a and target_b end up being the same.)

we see that the mean distances for target_a and target_b are less than random even using this naive euclidean distance metric; i.e. the embedding space is capturing positions that are closer than random pairs.

easy ( & hard ) positive ( & negative ) mining

N classes and the hard negative mining problem

let's go back to thinking about just triplet loss; specifically the common use case of wanting to learn embeddings for instances across N classes.

for the N class problem...

• the anchor is any random instance
• the positive is another instance from the same class
• the negative is any instance from any other class

in this setup there is a common problem involving the selection of negatives. for any particular anchor there will be many more negatives than positives so as we progress learning we'll see more and more of these negatives being cases that already satisfy the distance constraint. if we're just randomly picking triples we'll end up picking more and more that don't offer anything towards learning (i.e. have zero loss) we call these "easy" negatives. what we really want to do is focus on picking the fewer "hard" negatives. but how do we know what the hard ones are?

in the N class setup there are a number of approaches to mining hard negatives; the In Defense of the Triplet Loss for Person Re-Identification paper has some great information in section 2 on two online hard triple mining variants called BatchHard and BatchAll for the N class problem (though we won't describe them here)

explicit hard negatives (and positives) in the grasping setup

do we see this problem of "easy" triples in the grasping setup? oh yes. consider the following graph which shows the number of elements in a batch (of size 16) that have non zero loss.

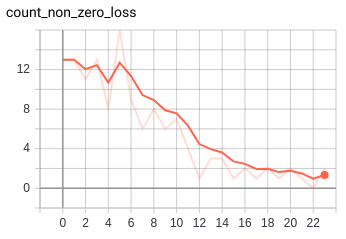
we can see that by the 15th step we're at the point of having only 1 or 2 (sometimes 0!) instances in a batch that have non zero loss (i.e. bulk of the batch has zero loss and so is contributing nothing to the training)

can we use BatchHard or BatchAll in the grasping setup? sadly, not really since the relationship between the anchors, positives and negatives are different. it's ok though as there are more explicit ways of describing hard triplets in our setup.

for the negatives it's about time; the closer in time a negative is to the anchor, the harder it's going to be to discriminate. a small change in time => similar camera image => similar embedding, but we want them to be different.

for the positives it's about camera location; the closer the postive camera is to the anchor the easier it is. a large change in camera position => different camera image => different embedding, but we want them to be the same.

given this we have two ways of increasing the difficulty of learning the embeddings.

• pick negatives closer in time to the anchor
• pick positives using a camera angle further from the anchor

comparing easy vs hard negatives

we can try a couple of experiments then regarding the choice of negatives

• a baseline case where negatives are chosen as any frame in a run
• when the negative example is chosen to be within 100 frames of the anchor
• when the negative example is chosen to be within 10 frames of the anchor

choosing the negative within 10 frames is quite difficult as the negative looks very similar to the anchor so it's perhaps unsurprising that training a model from scratch with these negatives fails a lot ( the failure mode being that all embeddings collapse to a single point ). we don't see this failure with the totally randomly chosen frames.

interestingly it seems that we are able to anneal at least and by training on the random frames for awhile and then switching to harder case. this works and is stable.

TODOs

as always i've gotten distracted by something else in the short term... for now at least the TODOs i want to play around with relate to avoid the wasted zero loss cases related to easy triples...

offline negative mining

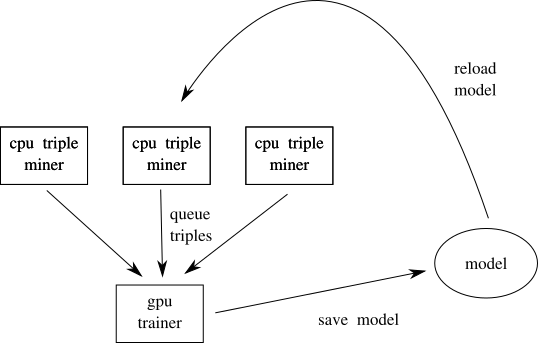
if our main goal is to keep a training loop busy doing useful work (i.e. minimising zero loss cases) we can farm out the checking of triples to a fleet of workers. these workers can randomly (or otherwise) sample triples against a reference model and only send triples to a central trainer if they don't look easy. this is something that parallelises well and we don't care necessarily about having these workers fast so it's a great fit for preemptiable cpu instances (remember performance != scalability) it's fine to have these workers use a slightly stale model for their reference and just update on some schedule.

replay buffers

additional to the offline mining another win would be to borrow an idea from from offline reinforcement learning; the replay buffer. if we mine triples we can use them to populate a replay buffer and then sample training batch from the replay buffer. the simplest approach would be to treat the buffer as a FIFO queue and expire entries based on time. more complex approaches can use the importance sampling ideas to keep examples around while they continue to add value to training.

i saw huge wins by implementing Prioritised Experience Replay for my Malmomo project

hard positives

the above talks about hard negatives and hard positives but i only trained hard negatives; i should do some more work on the mining of explicit hard positives.

train an actual grasping model!

the entire point of me starting this project was to try to train a grasping model but i haven't got there yet o_O

as things are i get the feeling this embedding might be capturing something about the arm but not really anything about the objects. still an open question...

code

all the code for this is on github