brain of mat kelcey...
cartpole++
August 11, 2016 at 10:00 PM | categories: projectsone of the classic control problems of reinforcement learning is the cartpole; the oldest reference to which i can find is Barto, Sutton & Anderson's "Neuronlikw Adaptive Elements That Can Solve Difficult Learning Control Problems (1983)
it's a simple enough sounding problem; given a cart in 2d, with a pole balancing on it, move the cart left and right to keep the pole balanced (i.e. within a small angle of vertical).
the entire problem can be described by input 4 variables; the cart position, the cart velocity, the pole angle, the pole angular velocity but even still it's surprisingly difficult to solve. there are loads of implementations of it and if you want to tinker i'd highly recommend starting with openai's gym version
as soon as you've solved it though you might want to play with a more complex physics environment and for that you need a serious physics simulator, e.g. the industry standard (and fully open sourced) bullet physics engine.
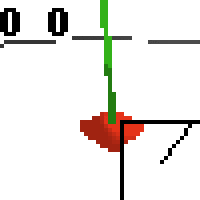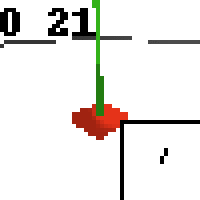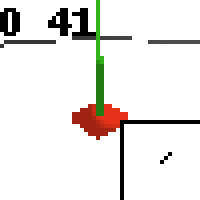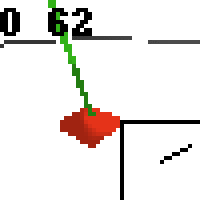
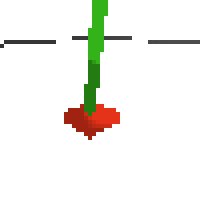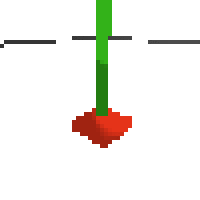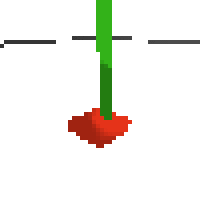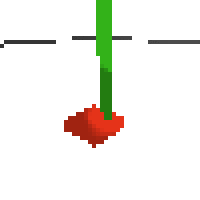
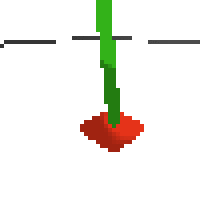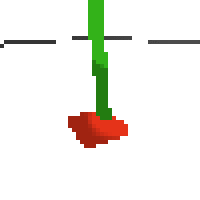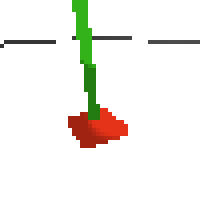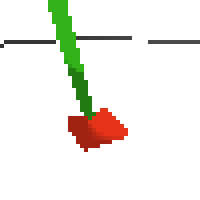
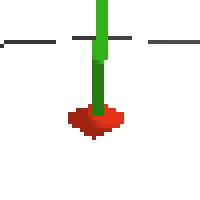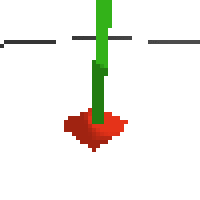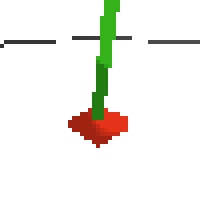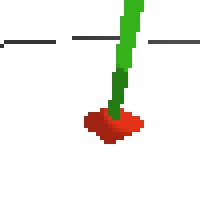
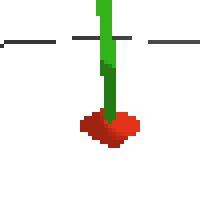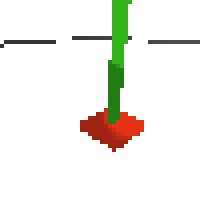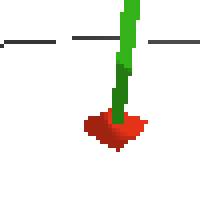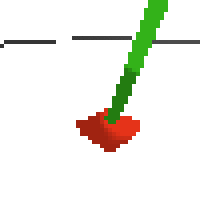
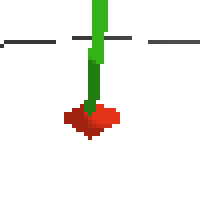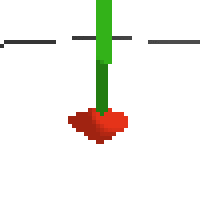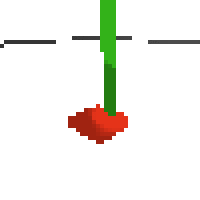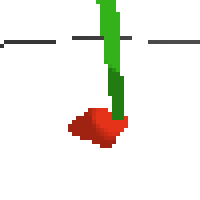
the simplest cartpole i could make includes 1) the ground 2) a cart (red) and 3) a pole (green). the blue line here denotes the z-axis. ( all code and repro instructions are on github )
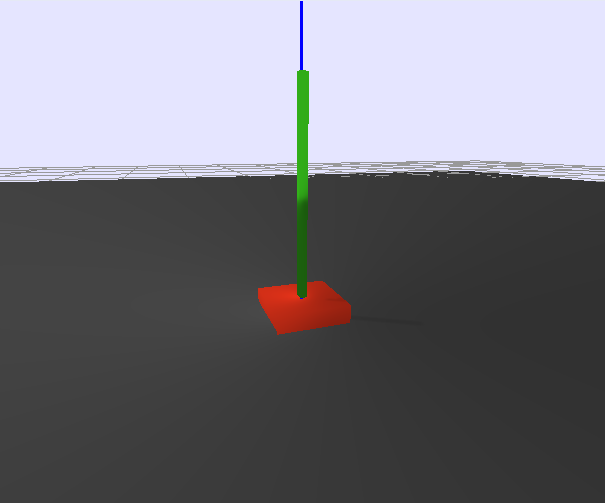
- the cart and pole move in 3d, not 1d.
- the pole is not connected to the cart (and since it's relatively light it makes from some crazy dynamics...)
- each run is started with a push of the cart in a random direction.
state representation
there are two state representations available; a low dimensional one based on the cart & pole pose and a high dimensional one based on raw pixels.
in both representations we use the idea of action repeats; per env.step we apply the choosen action 5 times, take a state snapshot, apply the action another 5 times and take another snapshot. the delta between these two snapshots provides enough information to infer velocity (if the learning algorithm finds that useful to do )
- the low dimensional state is (2, 2, 7)
- axis=0 represents the two snapshots; 0=first, 1=second
- axis=1 represents the object; 0=cart, 1=pole
- axis=2 is the 7d pose; 3d postition + 4d quaternion orientation
- this representation is usually just flattened to (28,) when used
- the high dimensional state is (50, 50, 6)
[:,:,0:3](the first three channels) is the RGB of a 50x50 render at first snapshot[:,:,3:6](the second three channels) is the RGB of a 50x50 render at the second snapshot- ( TODO: i concatted in the channel axis for ease of use with conv2d but conv3d is available and i should switch )
an example of the sequence of 50,50 renderings as seen by the network is the following (though network doesn't see the overlaid debugging info)
control
there are two basic methods for control; discrete and continuous
- the discrete control version uses 5 discrete actions; don't push, push up, down, left, right
- ( i've included a "dont move" action since, once the pole is balanced, the best thing to do is stop )
- the continuous control version uses a 2d action; the forces to apply in the x & y directions.
rewards
reward is just +1 for each step the pole is still upright
random agent
running this cartpole simulation with random actions gives pretty terrible performance with either random discrete or continuous control. we're lucky to get 5 or 10 steps (of a maximum 200 for our episode) in the video each time the cart skips back to the center represents the pole falling out of bounds and the sim reseting.
discrete control; low dimensional
- 5 actions; go left, right, up, down, do nothing
- state is cart & pole poses
training a deep q network
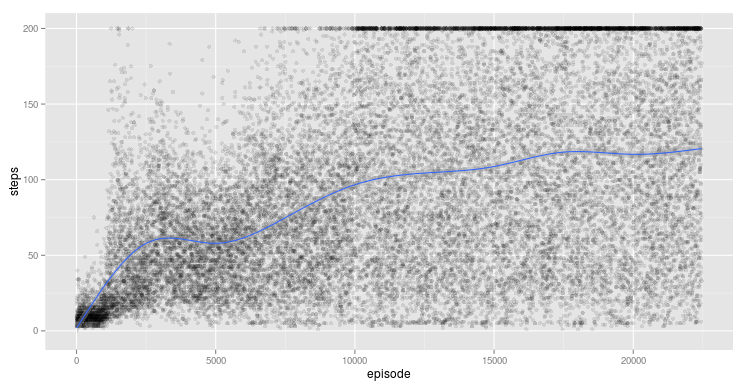
after training a vanilla dqn using kera-rl we get reasonable controller
the training curve is what we expect; terrible number of steps at the start then gradually getting a reasonable number of full runs (steps=200). still never gets to perfect runs 100% of the time though. there's also an interesting blip around episode 1,000 where it looked like it was doing OK and then diverged and recovered by about episode 7,500.
training with likelihood ratio policy gradient
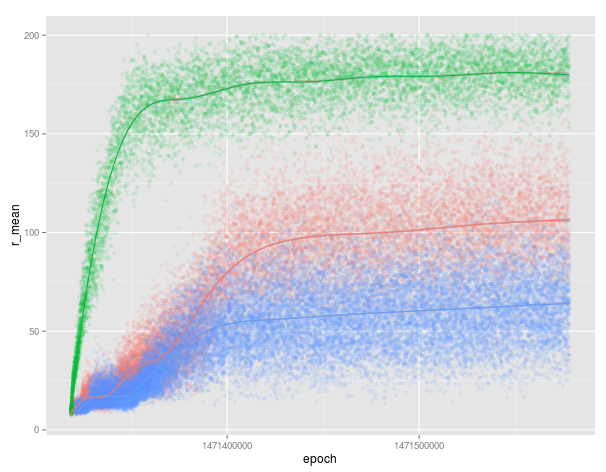
training with a baseline likelihood ratio policy gradient algorithm works well too... after 12 hrs it's getting 70% success rate keeping the pole balanced.
seems very sensitive to the initialisation though; here's three runs i started at the same time. it's interesting how much quicker the green one was getting good results....
what's really interesting is looking at what the blue (and actually red) models are doing....
whereas the green one (in the video above) is constantly making adjustments these other two models (red and blue) are much happier trying to stay still, i.e. long sequences of a 0 action. if they manage to get it balanced, or even nearly so, they just stop. this prior of 0 means though that if it's not balanced and they wait too long they haven't got time to recover. that's really cool! digging a bit further we can see that early in training there were cases where it manages to balance the pole very quickly and then just stopping for the rest of the episode. these were very successful, compared to other runs in the same batch, and hence this prior formed; do nothing and get a great (relative) reward! it's taking a loooong time for them to recover from these early successes and, eventually, they'll have an arguably better model at convergence.
here's the proportions of actions per run for the cases where the episode resulted in a reward of 200 (i.e. it's balanced). notice how the red and blue ones don't do well for particular initial starts, these correspond to cases where the behaviour of "no action" overwhelms particular starting pushes.
| run | stop | left | right | up | down |
|---|---|---|---|---|---|
| green | 0.32 | 0.16 | 0.15 | 0.22 | 0.13 |
| red | 0.65 | 0.12 | 0.00 | 0.11 | 0.10 |
| blue | 0.80 | 0.11 | 0.00 | 0.00 | 0.08 |
continuous control; low dimensional
- 2d action; force to apply on cart in x & y directions
- state is cart & pole poses
training with deep deterministic policy gradient
Continuous control with deep reinforcement learning introduced an continuous control version of deep q networks using an actor/critic model.
my implementation for this problem is ddpg_cartpole.py and it learns a reasonable policy though for the few long runs i've done it diverges after awhile. (i've also yet to have this run stable with raw pixels (probably bugs in my code no doubt))
continuous control; high dimensional
- 2d action; force to apply on cart in x & y directions
- state is 2 50x50 RGB images
training with normalised advantage functions
Continuous Deep Q-Learning with Model-based Acceleration introduced normalised advantage functions.
my implementation is naf_cartpole.py and i've found NAF to be a lot easier/stable to train than DDPG.
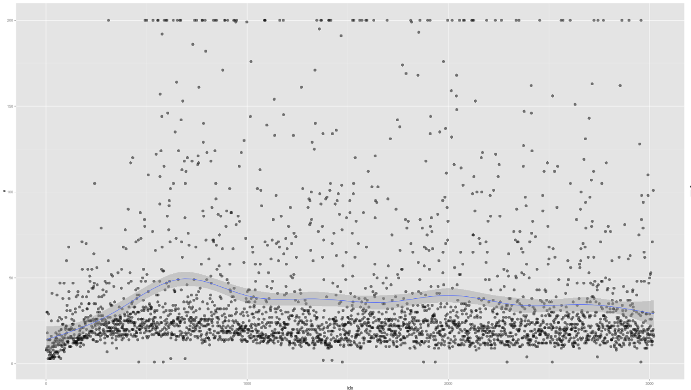
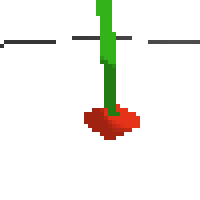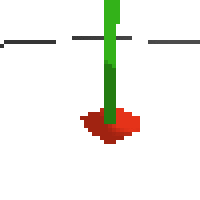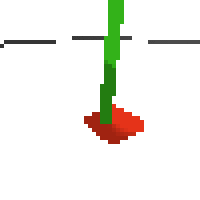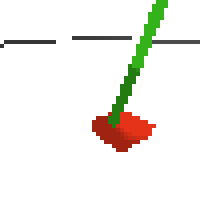
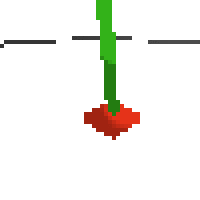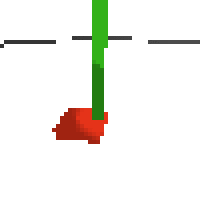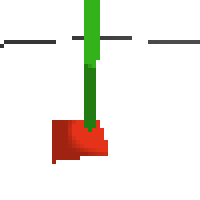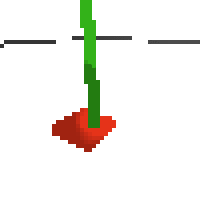
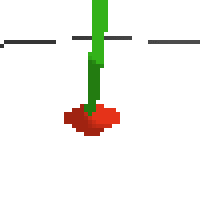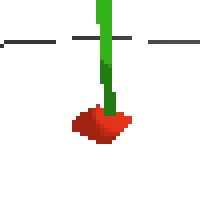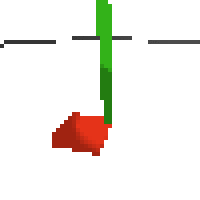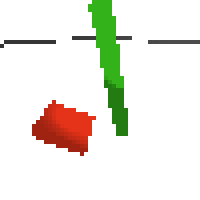
based on raw pixels i haven't yet got a model that can balance most of the time. it's definitely getting somewhere though if we look at episode length over time. (caps out at 200 which is the max episode length)
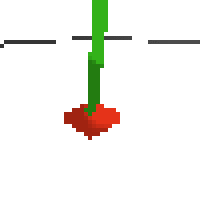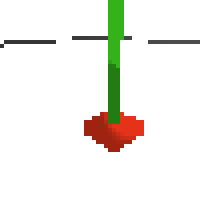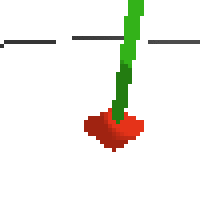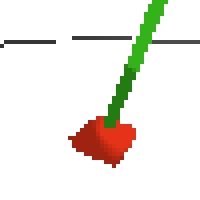
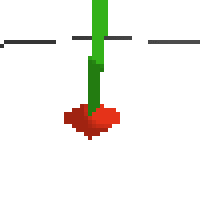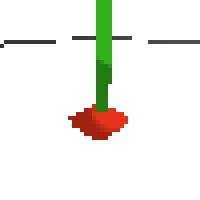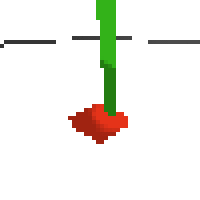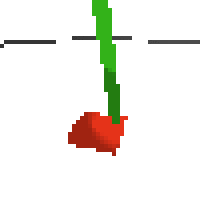
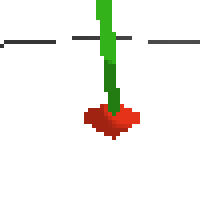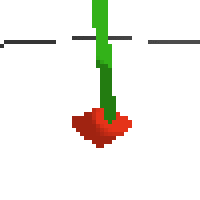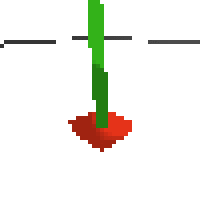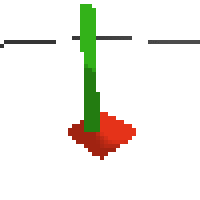
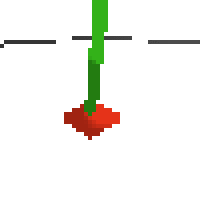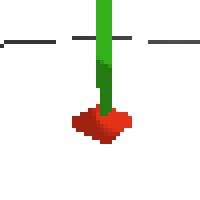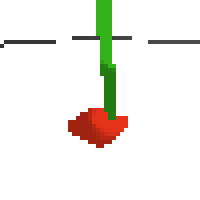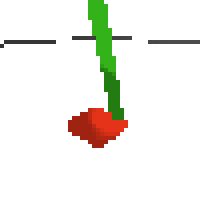
here's an example of NAF at the start of training. note: these are the 50x50 images as seen by the conv nets
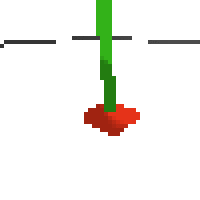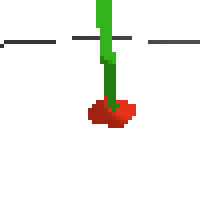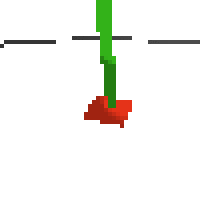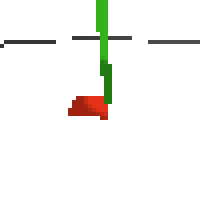
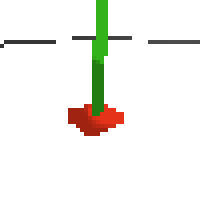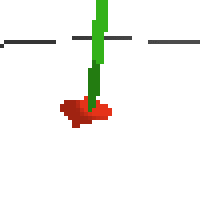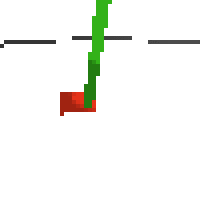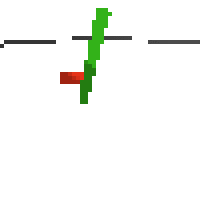
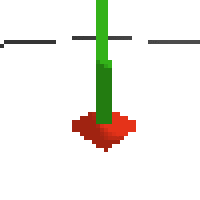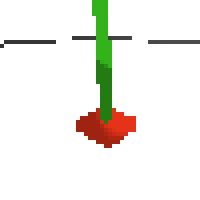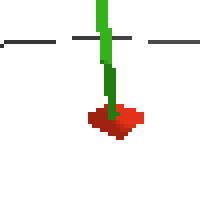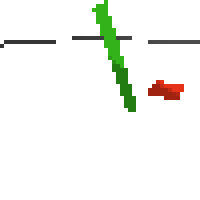
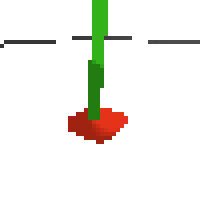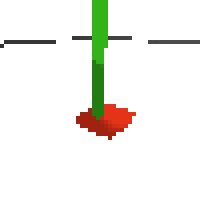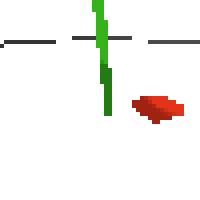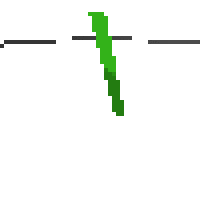
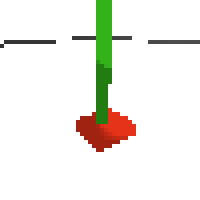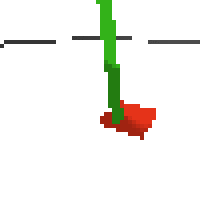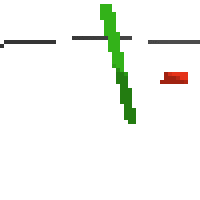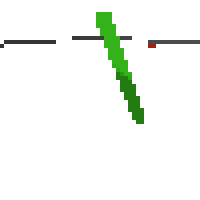
here's some examples of eval after training for 24hrs. i can still see mistakes so it should be doing better :/
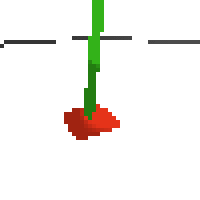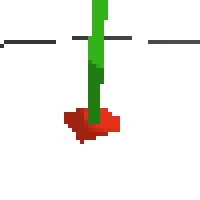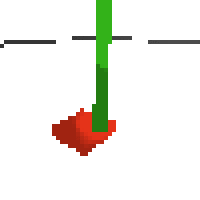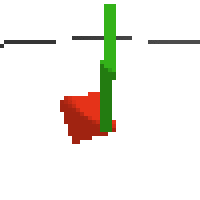


next steps
anyways maybe balancing on a cart is too boring; what about on a kuka arm :)






