what is cartpole?

ahhhh, good old cartpole, a favorite for baselining reinforcement learning algorithms! for those that haven't seen it the cartpole is a simple, but not completely trivial, control problem where an agent must keep an inverted pendulum balanced by nudging a cart either left or right.

the openai gym version is based on an observation of 4 values (the position / velocity of the cart & the angle / tip velocity of the pole) where the environment awards +1 reward for every time step the pendulum is kept up and terminates when either 1) the pole is angled too far off vertical 2) the cart moves too far from it's starting position or 3) 200 time steps have passed.

for this experiment we'll run trials using this environment where we attempt the problem 10 times, this gives a max possible reward score of 2,000. note: a score of 1950 would pass as 'solved' according to the definition of this environment.

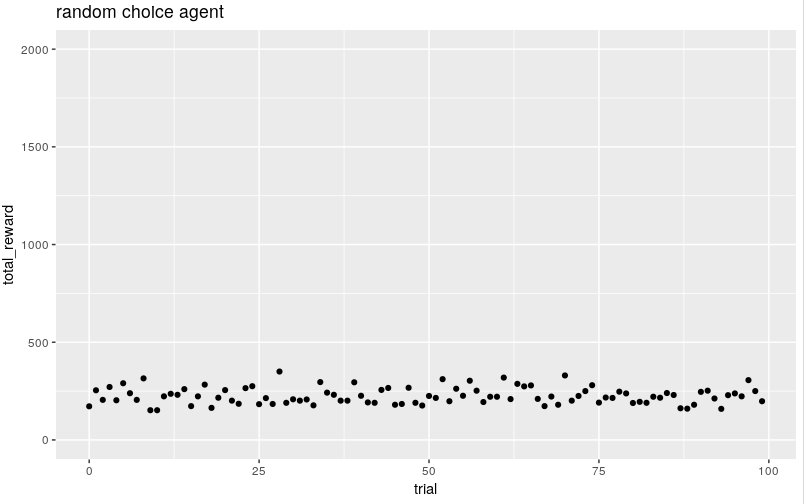
a random action baseline

as a baseline we'll use a random agent that nudges left/right randomly. as expected it's not great. running 100 trials the median is about ~220

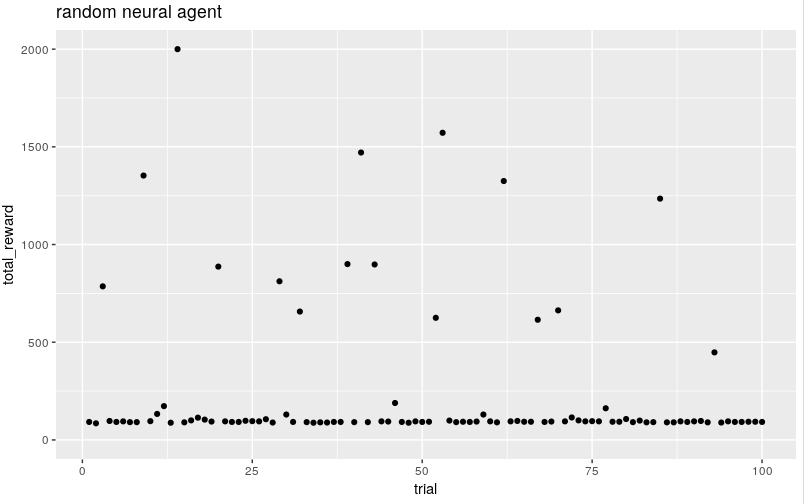
a random network baseline

let's try to represent the control using a simple network of 19 parameters

Layer (type)     Output Shape   Param #
========================================
i (InputLayer)   [(None, 4)]    0        # 4d input
h1 (Dense)       (None, 2)      10       # 2 node hidden (relu)
h2 (Dense)       (None, 2)      6        # 2 node hidden (relu)
o (Dense)        (None, 1)      3        # P(nudge_left)
========================================
Total params: 19

when we try random initialisations of this network we see it generally does worse than the random action, the median is now 95, but occasionally does much better. recall the environment says a sustained score of 1950 is solved.

will those occasional wins be enough signal to capture with an optimisation?

the covariance matrix adaptation evolution strategy

rather than training this network with the traditional RL approach let's try to evolve a solution using an evolutionary strategy!

we'll start with the covariance matrix adaptation evolution strategy CMS-ES ( using the cma lib )

as for all evolutionary approaches one main thing to decide is what representation to use. a key design aspect of CMA is that solutions are just samples from a multivariate normal & this actually works well for our problem, we'll just have solutions in R^19 representing the 19 weights and biases of the network.

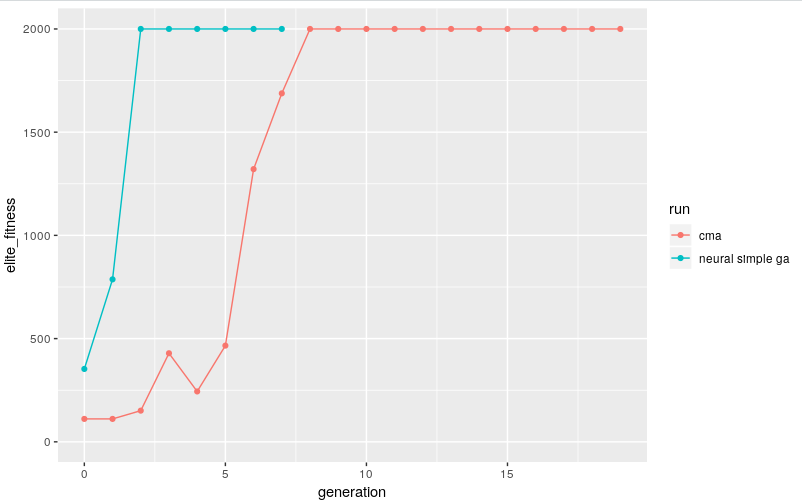
if we evolve a population of 20 members and plot the performance of the elite member from each generation we get a "solved" solution after only about 8 generations..

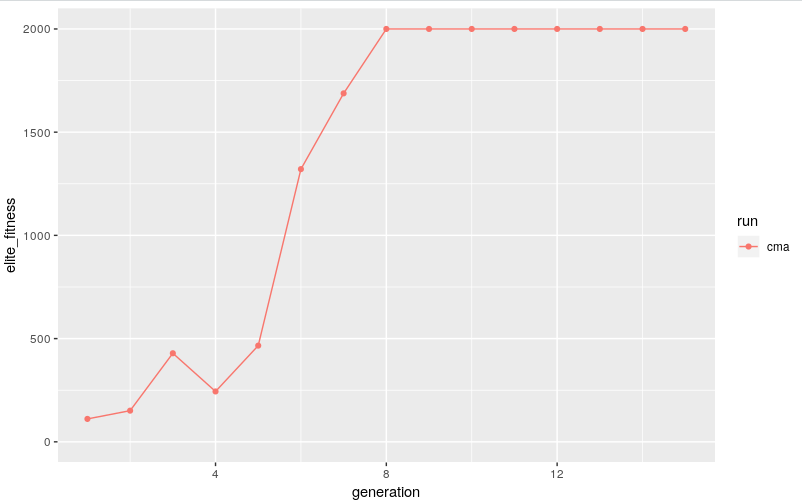
with a population size of 20 that's only 160 trials, not bad! to be honest in the past i'd collected x10 that #samples with a random agent when filling a replay buffer before any deep RL attempt o_O

simple genetic algorithm for the 19 weights

the CMA approach works but, for reasons we'll come back to, let's try it using a simpler style of genetic algorithm.

we'll start with an initial population whose weights come directly from the initialised keras model, but we'll evolve them using just a standard genetic algorithm using just a crossover operator

image from wikipedia

the simplest genetic algorithm requires only two things from us...

1. the ability to be able to generate new members
2. an implementation of the crossover function that takes two "parent" members and generates two valid new "children"

note: we'll use a really simple crossover operator; pick a random crossover point and combine the first part of one parent and the second part of the other. for a fixed length representation, like the 19 weights, this generates valid children without us having to do anything else. not all representations automatically do this; e.g. have a think about a representation for the travelling salesman problem that is just a random ordering of the cities...

we'll use a population of 20 again and for each generation we'll

• keep the 2 best performing members (elitism)
• introduce 2 completely new members (diversity)
• "breed" the remaining 18 using crossover

in particular we won't do any form of mutation or inversion which are common operators for genetic algorithms. they would be ok with this representation, but we'll leave them off to make things easier later.

though this is a very simple approach it works well and for this problem finds a solution faster than CMA; only 3 generations (60 trials)

digression : exporting a tf-lite network to a microcontroller

seemingly randomly, let's consider tf-lite for a bit....

tf-lite is a light weight tensorflow runtime for on device inference. the big focus is for mobile but it includes (experimental) support for microcontrollers too.

the approach to building a model for a microcontroller isn't trivial but isn't that hard either...

• train a standard keras model using whatever technique we want
• optimise the model (e.g. applying quantisation etc) in this case using tf.lite.Optimize.OPTIMIZE_FOR_SIZE
• use the lite converter to convert the model to flatbuffer format
• and finally, since microcontrollers don't provide a filesystem, use a tool like xxd to export the model as a byte[] we can use directly in c++ code. #l33tHax0r

for our simple network we get a 1488 element byte array like the following. this is the code we'd cut and paste into our microcontroller code.

unsigned char example_tflite_exported_network[] = {
  0x1c, 0x00, 0x00, 0x00, 0x54, 0x46, 0x4c, 0x33, 0x00, 0x00, 0x12, 0x00,
  0x1c, 0x00, 0x04, 0x00, 0x08, 0x00, 0x0c, 0x00, 0x10, 0x00, 0x14, 0x00,
  0x00, 0x00, 0x18, 0x00, 0x12, 0x00, 0x00, 0x00, 0x03, 0x00, 0x00, 0x00,
  0xe4, 0x05, 0x00, 0x00, 0xb8, 0x01, 0x00, 0x00, 0xa0, 0x01, 0x00, 0x00,
  0x34, 0x00, 0x00, 0x00, 0x04, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00,
  0x04, 0x00, 0x00, 0x00, 0xb8, 0xfa, 0xff, 0xff, 0x08, 0x00, 0x00, 0x00,
  0x0c, 0x00, 0x00, 0x00, 0x13, 0x00, 0x00, 0x00, 0x6d, 0x69, 0x6e, 0x5f,
  .....

two interesting observations about this pipeline are ....

1. we can use these steps to generate random initialised keras models which we can then convert to byte arrays (generating new members)
2. since these representations are fixed length a simple crossover operator of slicing one part of one parent and one part of the other automatically generates a byte array that is still a valid tflite flatbuffer

so... could this bytes array be used as a representation for our simple genetic algorithm? sure can!

simple genetic algorithm for the 1.4KB bytes of an exported tf-lite model

running our simple genetic algorithm against the bytes of these files works pretty much just as well as against the "raw" 19 weights, just a bit slower...

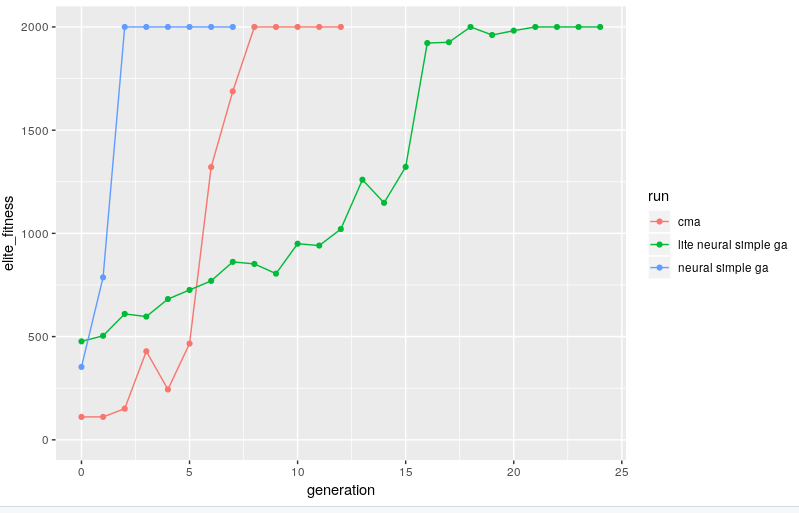
why slower? consider the binary diffs below between two elite members across generations. since it's the raw binary format there are huge chunks of the representation aren't actually weights but instead are related to the serialisation of network architecture. in terms of the genetic operators we could think of these as a bit like junk dna. the simple genetic algorithm "wastes time" exploring crossover in these regions which are effectively constant across the population. because we never use a mutation or inversion operator though we don't ever interfere with these and accidentally make infeasible solutions (which, incidentally, causes the python process to segfault when you try to create the interpreter :/)

finally do the models run on a microcontroller? yep :)

( though i was too lazy to actually hook them up to a serial connection and/or LEDs )

see all the code here