brain of mat kelcey...

previously i've discussed dimensionality reduction using SVD and PCA but another interesting technique is using a random projection.

in a random projection we project A (a NxM matrix) to A' (a NxO, O < M) by the transform AP=A' where P is a MxO matrix with random values.
( well not totally random, each column must have unit length (ie entries in each column must add to 1) )

though the results of this reduction are generally not as good as the results from SVD or PCA it has two huge benefits

• can be done without needing to hold P in memory (since it's entries can be generated multiple times using a seeded RNG)
• and more importantly it's really fast

how good is it compared to PCA i wonder? let's have a play around...

consider the 2d dataset of two clear clusters of points around (2,2) and (8,8)

the following shows 5 random projections to 1d compared to a 1d PCA reduction (done using weka)

there was a clear seperation between the 2 classes in 2d and it's retained in 3 out of the 5 projections even though we're using half the space going from 2d to 1d.
( the 2nd random projection actually looks very similiar to PCA )

what about some higher dimensions?

let's generate the same two clusters but in 10d; ie around the points (2,2,2,2,2,2,2,2,2,2) and (8,8,8,8,8,8,8,8,8,8)

though we can't plot this easily there are 2 useful visualisations of the data

a scatterplot, which is pretty uninteresting actually...

or a 2d tour through the 10d space

(check out my screencast on ggobi if you're after a better idea of what this tour represents)

lets compare 5 random projections to PCA when projecting from 10d to 1d
this time not so good... only one projection gets the clusters seperated, and only just.

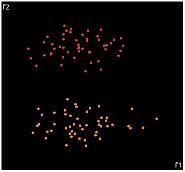
what about projecting to 2d?

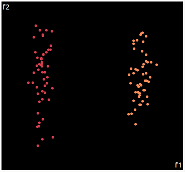
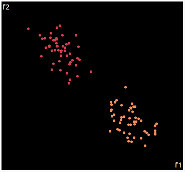
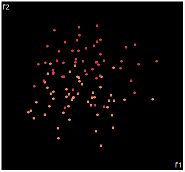
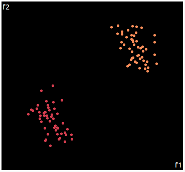
PCA	run1	run2	run3	run4	run5

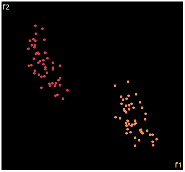PCA is by the cleanest with the x-axis representing the clusters and the y-axis representing the in cluster variance.
it clearly shows how the dataset can be projection to 1d, we only needed the first (x-axis) principal component.

the projections aren't too bad, all but 1 of them has the 2 clusters linearly seperable.

so in summary i think it's pretty good if you need to do something super fast. in these experiments i was using a pretty contrived dataset but was trying to be quite aggressive in going from 10d to 1d.

i wonder what, if any, difference there would be with sparse data?

< random evening hackery />