multi spectral channel data

eurosat/all is a dataset of 27,000 64x64 satellite images taken with 13 spectral bands. each image is labelled one of ten classes.

for the purpose of classification these 13 aren't equally useful, and the information in them varies across resolutions. if we were designing a sensor we might choose to use different channels in different resolutions.

how can we explore the trade off between mixed resolutions and whether to use a channel at all?

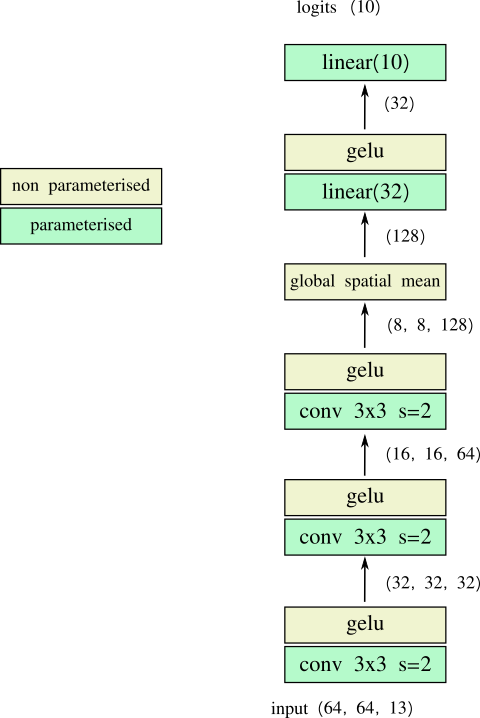
a simple baseline model

let's start with a simple baseline to see what performance we get. we won't spend too much time on this model, we just want something that we can iterate on quickly.

the simple model shown below trained on a 'training' split with adam hits 0.942 top 1 accuracy on a 2nd 'validation' split in 5 epochs. that'll do for a start.

what is the benefit of each channel?

let's check the effect of including different combos of input channels. we'll do so by introducing a channel mask.

a mask of all ones denotes using all channels and gives our baseline performance

mask	validation accuracy
[1,1,1,1,1,1,1,1,1,1,1,1,1]	0.942

a mask of all zeros denotes using no channels and acts as a sanity check; it gives the performance of random chance which is in line with what we expect give the balanced training set. (note: we standardise the input data so that it has zero mean per channel (with the mean, standard deviation parameters fit against training data only) so we can get this effect)

mask	validation accuracy
[1,1,1,1,1,1,1,1,1,1,1,1,1]	0.942
[0,0,0,0,0,0,0,0,0,0,0,0,0]	0.113

but what about if we drop just one channel? i.e. a mask of all ones except for a single zero.

channel to drop	validation accuracy
0	0.735
1	0.528
2	0.661
3	0.675
4	0.809
5	0.724
6	0.749
7	0.634
8	0.874
9	0.934
10	0.593
11	0.339
12	0.896

from this we can see that the performance hit we get from losing a single channel is not always the same. in particular consider channel 11; if we drop that channel we get a huge hit! does that mean that if we keep only 11 that should give reasonable performance?

mask	validation accuracy
[1,1,1,1,1,1,1,1,1,1,1,1,1]	0.942
[0,0,0,0,0,0,0,0,0,0,0,0,0]	0.113
[0,0,0,0,0,0,0,0,0,0,0,1,0] (keep just 11)	0.260

bbbzzzttt (or other appropriate annoying buzzer noise). channel 11 is contributing to the classification but it's not being used independently. in general this is exactly the behaviour we want from a neural network but what should we do to explore the effect of not having this dependence?

dropping out channels

consider using a dropout idea, just with input channels instead of intermediate nodes.

what behaviour do we get if we drop channels out during training? i.e. with 50% probability we replace an entire input channel with 0s?

things take longer to train and we get a slight hit in accuracy...

dropout?	validation accuracy
no	0.942
yes	0.934

...but now when we mask out one channel at a time we don't get a big hit for losing any particular one.

channel to drop	validation accuracy
	no dropout	with dropout
0	0.735	0.931
1	0.528	0.931
2	0.661	0.936
3	0.675	0.935
4	0.809	0.937
5	0.724	0.934
6	0.749	0.931
7	0.634	0.927
8	0.874	0.927
9	0.934	0.927
10	0.593	0.927
11	0.339	0.933
12	0.896	0.937

evolving the channel selection

now that we have a model that is robust to any combo of channels what do we see if we use a simple genetic algorithm (GA) to evolve the channel mask to use with this pre trained network? a mask that represents using all channels will be the best right? right?

we'll evolve the GA using the network trained above but based on it's performance on a 3rd "ga_train" split using the inverse loss as a fitness function.

amusingly the GA finds that a mask of [1,1,0,1,0,0,0,1,1,0,1,0,1] does better marginally better than all channels, but only uses 1/2 of them!

mask	split	accuracy
[1,1,1,1,1,1,1,1,1,1,1,1,1] (all)	ga_validate	0.934
[1,1,0,1,0,0,0,1,1,0,1,0,1] (ga)	ga_validate	0.936

important note: we can imagine the best performance overall would be to have the GA evolve not the channels to use from this model, but the channels to use when training from scratch. this would though require a lot more model training, basically a full training cycle per fitness evaluation :( in the approach we describe here we only have to train a single model and then have the GA just run inference.

what about different resolutions?

taking the idea of channel selection a step further, what if we got the GA to not only decide whether to use a channel or not, but also what resolution it should be in?

consider some example images across resolutions....

example images (just RGB channels shown)
orig x64	x32	x16	x8

we could then weight the use of a channel based on resolution; the higher the resolution the more the channel "costs" to use, with not using the channel at all being "free".

to support this we can change the GA to represent members not as a string of {0, 1}s but instead a sequence of {0, x8, x16, x32, x64} values per channel where these represent...

resolution	description	channel cost
x64	use original (64, 64) version of input	0.8
x32	use a 1/2 res (32, 32) version of input	0.4
x16	use a 1/4 res (16, 16) version of input	0.2
x8	use a 1/8 res (8, 8) version of input	0.1
0	don't use channel	0

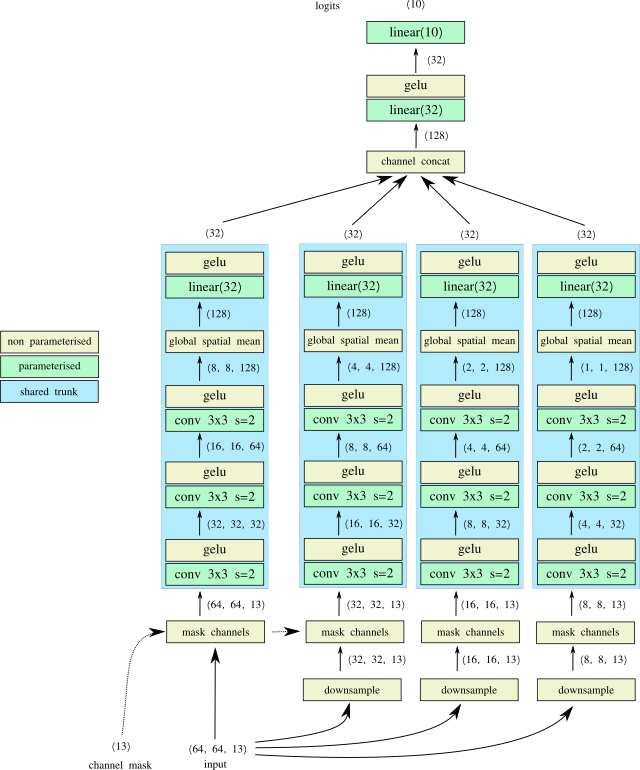
the change in the encoding of our GA is trivial, just 5 values per channel instead of 2, but before we look at that; how do we change our network?

we can do it without having to add too many extra parameters by using the magic of fully convolutional networks :)

notice how the main trunk of our first network was a series of 2d convolutions with a global spatial mean. this network will simply take as input all the resolutions we need! we can simply reuse it multiple times!

so we can have our network...

1. take the original x64 input
2. downsample it multiple times to x32, x16 and x8
3. mask out the channels so that each channel is only represented in one of the resolutions (or not represented at all if we want to ignore that channel)
4. run the main trunk network with shared parameters on each of the masked resolutions
5. combine the outputs with a simple channel concatenation
6. do one more non linear mixing (because, why not..)
7. finish with the logits

note: try as i might i can't get steps 2 to 4 to run parallelised in a pmap. asked on github about it and looks to be something you can't do at the moment.

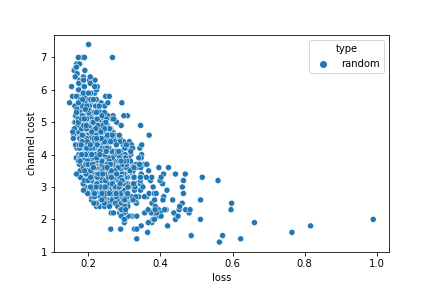
the channel cost vs loss pareto front

when we consider channel cost vs loss there is no single best solution, it's a classic example of a pareto front where we see a tradeoff between the channel_cost and loss.

consider this sampling of 1,000 random channel masks...

rerunning the GA

the GA needs to operate with a fitness that's a single scalar; for now we just use a simple combo of (1.0 / loss) - channel_cost

running with this fitness function we evolve the solution [x16, x64, x64, x16, x32, ignore, x8, x64, x8, ignore, x8, ignore, x32]

it's on the pareto front, as we'd hope, and it's interesting that it includes a mix of resolutions including ignoring 3 channels completely :)

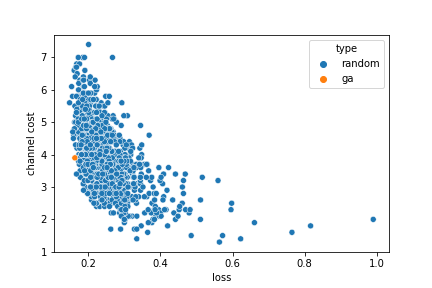
different mixings of loss and channel_cost would result in different GA solutions along the front

code

all the code is on github