out of distribution (OOD) detection

OOD detection is an often overlooked part of many projects. it's super important to understand when your model is operating on data it's not familiar with!

though this can be framed as the problem of detecting that an input differs from training data, discussed more in this 'data engineering concerns for machine learning products' talk, for this post we're going to look at the problem more from the angle of the model needing to be able to express it's own lack of confidence.

a core theme of this post is treating OOD as a function of the output of the model. when i've played with this idea before the best result i've had is from using entropy as a proxy of confidence. in the past it's not be in the context of OOD directly but instead as a way of prioritising data annotation (i.e. uncertainty sampling for active learning)

using entropy as a stable measure of confidence though requires a model be well calibrated.

neural net calibration

neural nets are sadly notorious for not being well calibrated under the default ways we train these days.

the first approach i was shown to calibrate a neural net is to train your model as normal, then finetune just the final classifier layer using a held out set; the general idea being that this is effectively just a logistic regression on features learnt by the rest of the network and so should come with the better guarantees that logistic regression provides us regarding calibration (see this great overview from sklearn) whereas this has always worked well for me it does require two steps to training, as well as the need for a seperate held out set to be managed.

another apporach to calibration i revisited this week comes from this great overview paper from 2017 on calibration of modern neural networks. it touches on platt scaling, which i've also used in the past successfully, but includes something even simpler i didn't really notice until it was pointed out to me by a colleague; don't bother tuning the entire last layer, just fit a single temperature rescaling of the output logits i.e. what can be thought of as a single parameter version of platt scaling. what a great simple idea!

the main purpose of this post though is to reproduce some ideas around out of distribution and calibration when you use focal loss. this was described in this great piece of work calibrating deep neural networks using focal loss. we'll implement that, but the other two as well for comparison.

( as an aside, another great simple way of determining confidence is using an ensemble! i explore this idea a bit in my post on ensemble nets where i train ensembles as a single model using jax vmap )

experiments

dataset

let's start with cifar10 and split the data up a bit differently than the standard splits...

1. we'll union the standard cifar10 train and test splits.
2. hold out instances labelled automobile & cat as a "hard" ood set ( i've intentionally chosen these two since i know they cause model confusion as observed in this keras.io tute on metric learning ).
3. split the remaining 8 classes into 0.7 train and 0.1 for each of validation, calibration and test.

we'll additionally generate an "easy" ood set which will just be random images.

in terms of how we'll use these splits...

• train will be the main dataset to train against.
• validation will be used during training for learning rate stepping, early stopping, etc.
• calibration will be used when we want to tune a model in some way for calibration.
• test will be used for final held out analysis.
• ood_hard and ood_easy will be used as the representative out of distribution sets.

examples images
in distribution
out of distribution (hard)
out of distribution (easy)

method overview

1. train a base model, model_1, on train, tuning against validate.
2. create model_2 by finetuning the last layer of model_1 against calibrate; i.e. the logisitic regression approach to calibration.
3. create model_3 by just fitting a scalar temperture of last layer of model_1; i.e. the temperture scaling approach.
4. train some focal loss models from scratch against train using validate for tuning.

at each step we'll check the entropy distributions across the various splits, including the easy and hard ood sets

model_1: baseline

for a baseline we'll use a resnet18 objax model trained against train using validate for simple early stopping.

# define model
model = objax.zoo.resnet_v2.ResNet18(in_channels=3, num_classes=10)
# train against all model vars
trainable_vars = model.vars()

$ python3 train_basic_model.py --loss-fn cross_entropy --model-dir m1

learning_rate 0.001 validation accuracy 0.372 entropy min/mean/max 0.0005 0.8479 1.9910
learning_rate 0.001 validation accuracy 0.449 entropy min/mean/max 0.0000 0.4402 1.9456
learning_rate 0.001 validation accuracy 0.517 entropy min/mean/max 0.0000 0.3566 1.8013
learning_rate 0.001 validation accuracy 0.578 entropy min/mean/max 0.0000 0.3070 1.7604
learning_rate 0.001 validation accuracy 0.680 entropy min/mean/max 0.0000 0.3666 1.7490
learning_rate 0.001 validation accuracy 0.705 entropy min/mean/max 0.0000 0.3487 1.6987
learning_rate 0.001 validation accuracy 0.671 entropy min/mean/max 0.0000 0.3784 1.8276
learning_rate 0.0001 validation accuracy 0.805 entropy min/mean/max 0.0000 0.3252 1.8990
learning_rate 0.0001 validation accuracy 0.818 entropy min/mean/max 0.0000 0.3224 1.7743
learning_rate 0.0001 validation accuracy 0.807 entropy min/mean/max 0.0000 0.3037 1.8580

we can check the distribution of entropy values of this trained model against our various splits

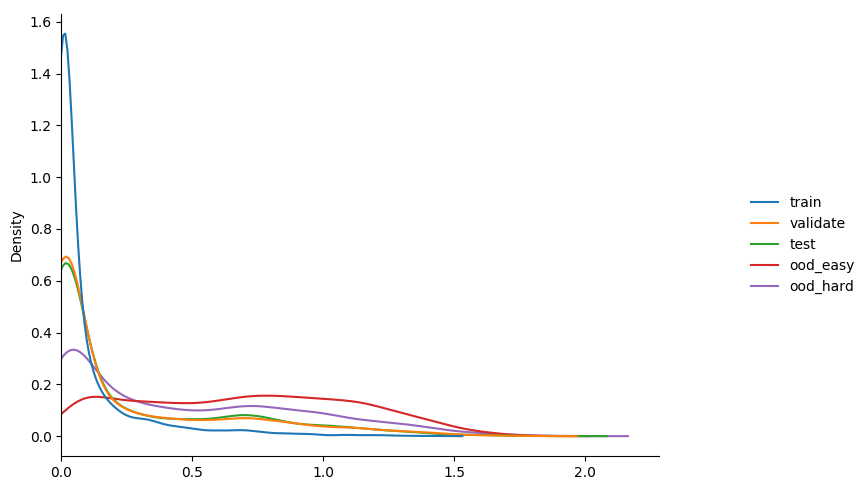
some observations...

• highest confidence, i.e. lowest entropy, on training set.
• equiv values on validation and test; both < training.
• ood lowest of all; this is a good thing!
• mean value of entropy on the validation set slowly drops over training.

recall that a higher entropy => a more uniform distribution => less prediction confidence.

as such our goal is to have the entropy of the ood set as high as possible without dropping the test set too much.

model_2: fine tuning entire classifier layer

as mentioned before the main approach i'm familiar with is retraining the classifier layer. we'll start with model_1 and use the so-far-unseen calibration set for fine tuning it.

# define model
model = objax.zoo.resnet_v2.ResNet18(in_channels=3, num_classes=10)
# restore from model_1
objax.io.load_var_collection('m1/weights.npz', model.vars())
# train against last layer only
classifier_layer = model[-1]
trainable_vars = classifier_layer.vars()

$ python3 train_model_2.py --input-model-dir m1 --output-model-dir m2

learning_rate 0.001 calibration accuracy 0.808 entropy min/mean/max 0.0000 0.4449 1.8722
learning_rate 0.001 calibration accuracy 0.809 entropy min/mean/max 0.0002 0.5236 1.9026
learning_rate 0.001 calibration accuracy 0.808 entropy min/mean/max 0.0004 0.5468 1.9079
learning_rate 0.001 calibration accuracy 0.811 entropy min/mean/max 0.0005 0.5496 1.9214
learning_rate 0.001 calibration accuracy 0.812 entropy min/mean/max 0.0001 0.5416 1.9020
learning_rate 0.001 calibration accuracy 0.812 entropy min/mean/max 0.0002 0.5413 1.9044
learning_rate 0.001 calibration accuracy 0.811 entropy min/mean/max 0.0003 0.5458 1.8990
learning_rate 0.001 calibration accuracy 0.814 entropy min/mean/max 0.0001 0.5472 1.9002
learning_rate 0.001 calibration accuracy 0.812 entropy min/mean/max 0.0001 0.5455 1.9124
learning_rate 0.001 calibration accuracy 0.813 entropy min/mean/max 0.0001 0.5503 1.9092
learning_rate 0.0001 calibration accuracy 0.813 entropy min/mean/max 0.0001 0.5485 1.9011
learning_rate 0.0001 calibration accuracy 0.814 entropy min/mean/max 0.0001 0.5476 1.9036
learning_rate 0.0001 calibration accuracy 0.813 entropy min/mean/max 0.0001 0.5483 1.9051
learning_rate 0.0001 calibration accuracy 0.813 entropy min/mean/max 0.0000 0.5479 1.9038
learning_rate 0.0001 calibration accuracy 0.813 entropy min/mean/max 0.0000 0.5482 1.9043
learning_rate 0.0001 calibration accuracy 0.813 entropy min/mean/max 0.0000 0.5482 1.9059
learning_rate 0.0001 calibration accuracy 0.813 entropy min/mean/max 0.0000 0.5479 1.9068
learning_rate 0.0001 calibration accuracy 0.813 entropy min/mean/max 0.0000 0.5480 1.9058
learning_rate 0.0001 calibration accuracy 0.812 entropy min/mean/max 0.0000 0.5488 1.9040
learning_rate 0.0001 calibration accuracy 0.814 entropy min/mean/max 0.0000 0.5477 1.9051

if we compare (top1) accuracy of model_1 vs model_2 we see a slight improvement in model_2, attributable to the slight extra training i suppose (?)

$ python3 calculate_metrics.py --model m1/weights.npz

train accuracy      0.970
validate accuracy   0.807
calibrate accuracy  0.799
test accuracy       0.803

$ python3 calculate_metrics.py --model m2/weights.npz

train accuracy      0.980
validate accuracy   0.816
calibrate accuracy  0.814
test accuracy       0.810

more importantly though; how do the entropy distributions looks?

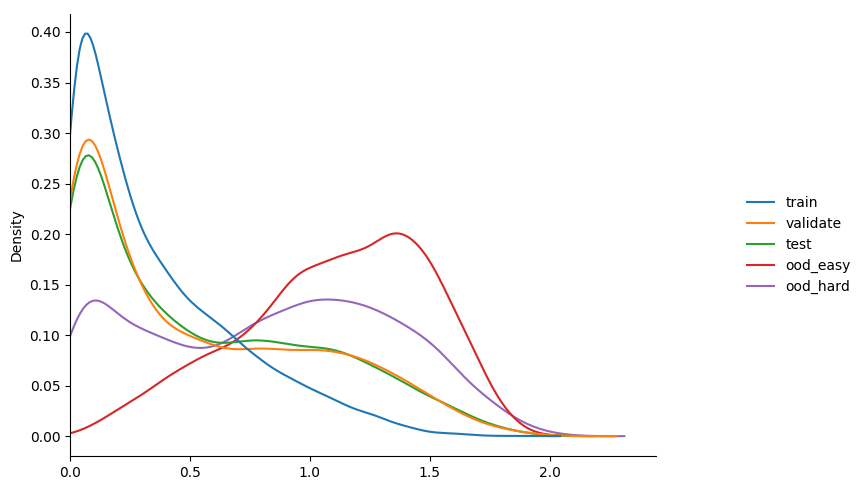
some observations...

• calibration accuracy and entropy during training shifted a bit, but not a lot.
• again highest confidence on training.
• again equiv values on validation and test; both < training.
• ood difference a bit more distinct now.

model_3: fit a scalar temperature value to logits

in model_3 we create a simple single parameter layer that represents rescaling, append it to the pretrained resnet and train just that layer.

class Temperature(objax.module.Module):
    def __init__(self):
        super().__init__()
        self.temperature = objax.variable.TrainVar(jnp.array([1.0]))
    def __call__(self, x):
        return x / self.temperature.value

# define model
model = objax.zoo.resnet_v2.ResNet18(in_channels=3, num_classes=10)
# restore from model_1
objax.io.load_var_collection('m1/weights.npz', model.vars())
# add a temp rescaling layer
temperature_layer = layers.Temperature()
model.append(temperature_layer)
# train against just this layer
trainable_vars = temperature_layer.vars()

$ python3 train_model_3.py --input-model-dir m1 --output-model-dir m3

learning_rate 0.01 temp 1.4730 calibration accuracy 0.799 entropy min/mean/max 0.0006 0.5215 1.9348
learning_rate 0.01 temp 1.5955 calibration accuracy 0.799 entropy min/mean/max 0.0013 0.5828 1.9611
learning_rate 0.01 temp 1.6118 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5911 1.9643
learning_rate 0.01 temp 1.6162 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5933 1.9652
learning_rate 0.01 temp 1.6118 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5911 1.9643
learning_rate 0.01 temp 1.6181 calibration accuracy 0.799 entropy min/mean/max 0.0015 0.5943 1.9655
learning_rate 0.01 temp 1.6126 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5915 1.9645
learning_rate 0.01 temp 1.6344 calibration accuracy 0.799 entropy min/mean/max 0.0016 0.6025 1.9687
learning_rate 0.01 temp 1.6338 calibration accuracy 0.799 entropy min/mean/max 0.0016 0.6022 1.9686
learning_rate 0.01 temp 1.6018 calibration accuracy 0.799 entropy min/mean/max 0.0013 0.5860 1.9623
learning_rate 0.001 temp 1.6054 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5878 1.9630
learning_rate 0.001 temp 1.6047 calibration accuracy 0.799 entropy min/mean/max 0.0013 0.5874 1.9629
learning_rate 0.001 temp 1.6102 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5903 1.9640
learning_rate 0.001 temp 1.6095 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5899 1.9638
learning_rate 0.001 temp 1.6112 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5908 1.9642
learning_rate 0.001 temp 1.6145 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5924 1.9648
learning_rate 0.001 temp 1.6134 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5919 1.9646
learning_rate 0.001 temp 1.6144 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5924 1.9648
learning_rate 0.001 temp 1.6105 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5904 1.9640
learning_rate 0.001 temp 1.6151 calibration accuracy 0.799 entropy min/mean/max 0.0014 0.5927 1.9650

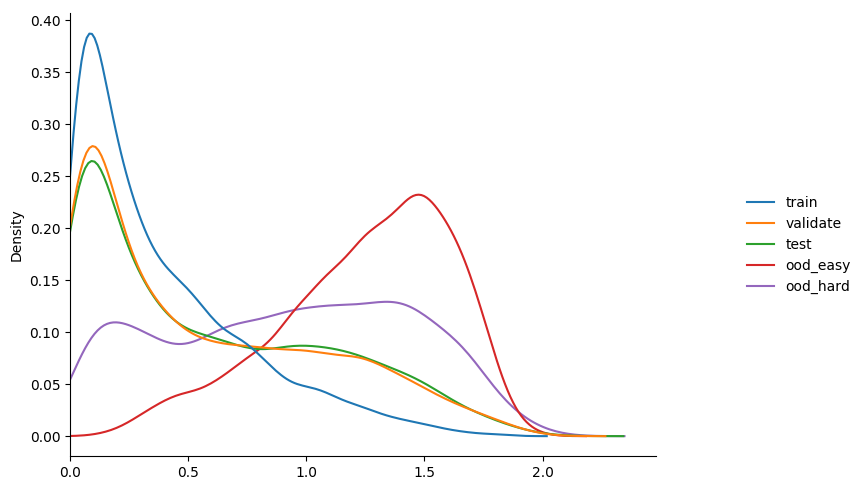
some observations...

• we're fitting a single value, so very fast!
• as expected we don't see any change in accuracy during training compared to model_1. this is since the temp rescaling never changes the ordering of predictions. ( just this property alone could be enough reason to use this approach in some cases! )
• slightly better than model_2 in terms of raising the entropy of ood!

not bad for fitting a single parameter :D

model_4: use focal loss

as a final experiment we'll use focal loss for training instead of cross entropy

note: i rolled my own focal loss function which is always dangerous! it's not impossible (i.e. it's likely) i've done something wrong in terms of numerical stability; please let me know if you see a dumb bug :)

def focal_loss_sparse(logits, y_true, gamma=1.0):
    log_probs = jax.nn.log_softmax(logits, axis=-1)
    log_probs = log_probs[jnp.arange(len(log_probs)), y_true]
    probs = jnp.exp(log_probs)
    elementwise_loss = -1 * ((1 - probs)**gamma) * log_probs
    return elementwise_loss

note that focal loss includes a gamma. we'll trial 1.0, 2.0 and 3.0 in line with the experiments mentioned in calibrating deep neural networks using focal loss

gamma 1.0

$ python3 train_basic_model.py --loss-fn focal_loss --gamma 1.0 --model-dir m4_1

learning_rate 0.001 validation accuracy 0.314 entropy min/mean/max 0.0193 1.0373 2.0371
learning_rate 0.001 validation accuracy 0.326 entropy min/mean/max 0.0000 0.5101 1.8546
learning_rate 0.001 validation accuracy 0.615 entropy min/mean/max 0.0000 0.6680 1.8593
learning_rate 0.001 validation accuracy 0.604 entropy min/mean/max 0.0000 0.5211 1.8107
learning_rate 0.001 validation accuracy 0.555 entropy min/mean/max 0.0001 0.5127 1.7489
learning_rate 0.0001 validation accuracy 0.758 entropy min/mean/max 0.0028 0.6008 1.8130
learning_rate 0.0001 validation accuracy 0.780 entropy min/mean/max 0.0065 0.6590 1.9305
learning_rate 0.0001 validation accuracy 0.796 entropy min/mean/max 0.0052 0.6390 1.8589
learning_rate 0.0001 validation accuracy 0.790 entropy min/mean/max 0.0029 0.5886 1.9151

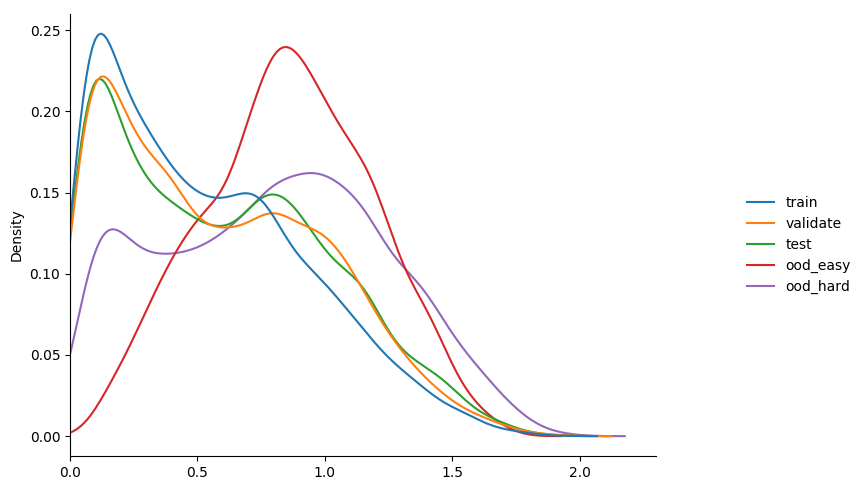
gamma 2.0

$ python3 train_basic_model.py --loss-fn focal_loss --gamma 2.0 --model-dir m4_2

learning_rate 0.001 validation accuracy 0.136 entropy min/mean/max 0.0001 0.2410 1.7906
learning_rate 0.001 validation accuracy 0.530 entropy min/mean/max 0.0000 0.8216 2.0485
learning_rate 0.001 validation accuracy 0.495 entropy min/mean/max 0.0003 0.7524 1.9086
learning_rate 0.001 validation accuracy 0.507 entropy min/mean/max 0.0000 0.6308 1.8460
learning_rate 0.001 validation accuracy 0.540 entropy min/mean/max 0.0000 0.5899 2.0196
learning_rate 0.001 validation accuracy 0.684 entropy min/mean/max 0.0001 0.6189 1.9029
learning_rate 0.001 validation accuracy 0.716 entropy min/mean/max 0.0000 0.6509 1.8822
learning_rate 0.001 validation accuracy 0.606 entropy min/mean/max 0.0001 0.7096 1.8312
learning_rate 0.0001 validation accuracy 0.810 entropy min/mean/max 0.0002 0.6208 1.9447
learning_rate 0.0001 validation accuracy 0.807 entropy min/mean/max 0.0004 0.6034 1.8420

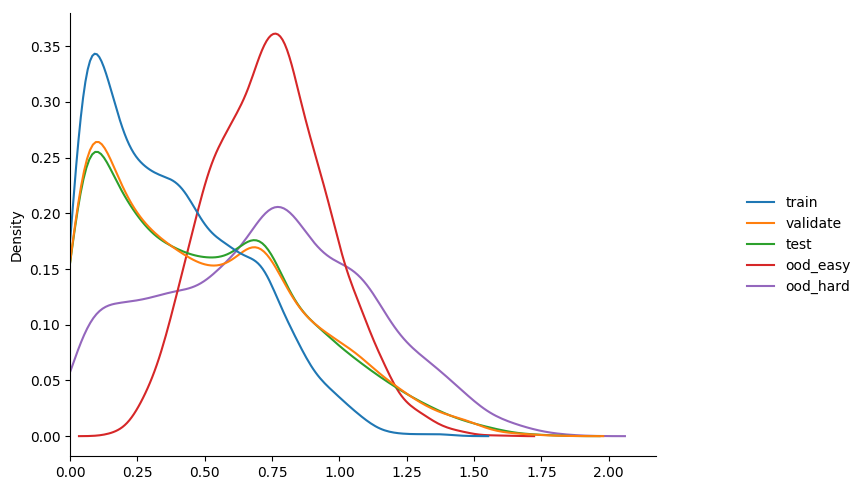
gamma 3.0

$ python3 train_basic_model.py --loss-fn focal_loss --gamma 3.0 --model-dir m4_3

learning_rate 0.001 validation accuracy 0.288 entropy min/mean/max 0.0185 1.1661 1.9976
learning_rate 0.001 validation accuracy 0.319 entropy min/mean/max 0.0170 1.0925 2.1027
learning_rate 0.001 validation accuracy 0.401 entropy min/mean/max 0.0396 0.9795 2.0361
learning_rate 0.001 validation accuracy 0.528 entropy min/mean/max 0.0001 0.8534 1.9115
learning_rate 0.001 validation accuracy 0.528 entropy min/mean/max 0.0002 0.7405 1.8509
learning_rate 0.0001 validation accuracy 0.748 entropy min/mean/max 0.0380 0.9204 1.9697
learning_rate 0.0001 validation accuracy 0.760 entropy min/mean/max 0.0764 0.9807 1.9861
learning_rate 0.0001 validation accuracy 0.772 entropy min/mean/max 0.0906 0.9646 2.0556
learning_rate 0.0001 validation accuracy 0.781 entropy min/mean/max 0.0768 0.8973 1.9264
learning_rate 0.0001 validation accuracy 0.780 entropy min/mean/max 0.0871 0.8212 1.9814

some observations...

• can see that immediately the model behaves more like model_2 than model_1 in terms of calibration.
• increasing gamma really starts to seperate the ood data, but with a drop in overall validation accuracy. maybe the seperation isn't as much as i'd like, but happy to experiment more given this result.

interesting!! focal loss is definitely going in my "calibration toolkit" :D

doing the actual detection though

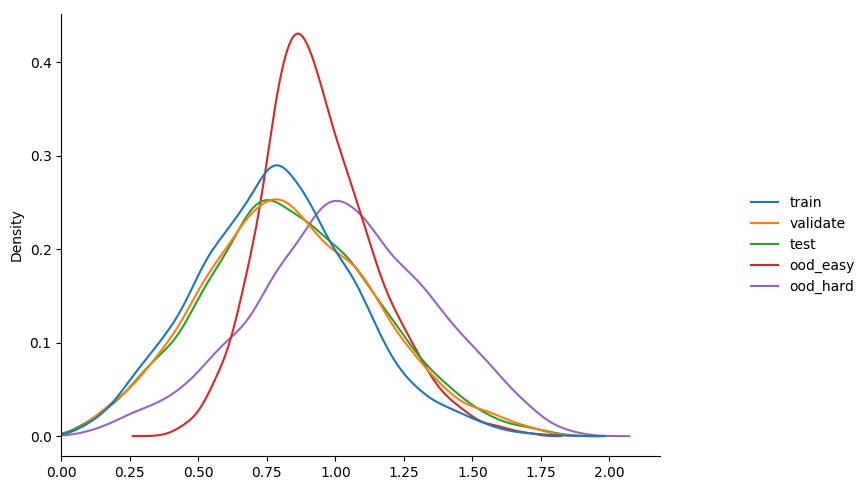
recall the distribution plot of entropies from the model_3 experiment

we can eyeball that the entropies values are low for in-distribution sets (train, validate, calibrate and test) and high for the two ood sets (easy and hard) but how do we actually turn this difference into a in-distribution classifier? ( recall this is not a standard supervised learning problem, we only have the in-distribution instances to train against and nothing from the ood sets at training time )

amusingly i spent a bunch of time hacking around with all sorts of density estimation techniques but it turned out the simplest baseline i started with was the best :/

the baseline works on a strong, but valid enough, assumption of the entropies; the entropies for in-distribution instances will be lower than the entropies for OOD instances. given this assumption we can just do the simplest "classifier" of all; thresholding

to get a sense of the precision/recall tradeoff of approach we can do the following...

• fit a MinMax scaler to the train set; this scales all train values to (0, 1)
• use this scaler to transform test, ood_easy and ood_hard; including (0, 1) clipping
• "flip" all the values, x = 1.0 - x, since we want a low entropy to denote a positive instance of in-distribution
• compare the performance of this "classifier" by considering test instances as positives and ood instances as negatives.

with this simple approach we get the following ROC, P/R and reliability plots.

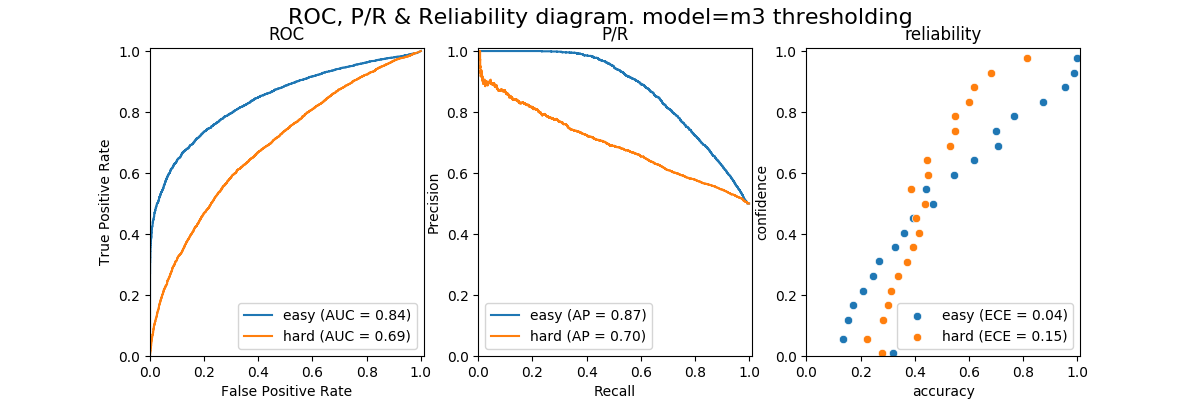
i've included the attempts i made to use a kernel density estimator in fit_kernel_density_to_entropy.py so if you manage to get a result better than this trivial baseline please let me know :)

other options for detecting OOD

though this post is about using entropy as a way of measuring OOD there are other ways too.

the simplest way i've handled OOD detection in the past is to include an explicit OTHER label. this has worked in cases where i've had data available to train against, e.g. data that was (somehow) sampled but wasn't of interest for actual supervised problem at hand. but i can see in lots of situations this wouldn't always be possible.

another approach i'm still hacking on is doing density estimation on the inputs; this related very closely to the diversity sampling ideas for active learning.

code

these experiments were written in objax, an object oriented wrapper for jax

code available on github